两正弦量求和方法(正弦量的相量表示法)
1.正弦量的相量表示法
去百度文库，查看完整内容>
内容来自用户：1975JGJ
4-1 正弦交流电路的分析方法
一、用向量表示正弦量
表示正弦量的方法：三角函数式、波形图、相量图（式）。
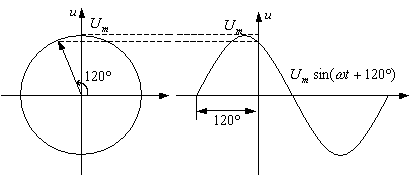
一、正弦量的旋转矢量表示
1、相量：在一平面直角坐标系上画一矢量，它的长度等于正弦量的最大值，它与横轴正方向之间的夹角为正弦量的初相，而角速度因是固定的也可不必再标明，这种仅反映正弦量的最大值和初相的“静止的”矢量，称为相量。如：、、。
有效值相量：表示出正弦量的有效值和初相位的相量。如：、、。
2、注意：⑴相同单位的量应按相同的的比例尺来画，不同单位的量可以用不同的比例尺来画；⑵只有同频率的正弦量才能画在同一相量图上，否则无法进行比较和运算。
二、同频率正弦量的加、减
确定和ψ可用曲线相加法，也可用相量作图法。
1、相量作图法的步骤：先用出相量和，而后以和为邻边作一平行四边形，其对角线即为合成电流的相量。的长度为有效值，与横轴正方向的夹角即为初相ψ。
2、应用相量作图法对正弦量进行减法时，实质与加法相同。
例如：
3、三角形法求矢量加、减
两矢量求和：两相量“头尾相连”，第三条边即是它们的和。
两矢量求差：两相量“尾尾相连，指向最减数的第三边即为它们的差。
多个相量相加时：各相量“头尾相连”，由第一个相量的箭尾和最后一个相量的箭头作一相量，即为求和的相量。一、正弦电路中电阻元件的电压和电流之间的关系如下：
2.电路：为什么同频正弦量的求和可用相量求和
相量只是一种表现形式，正弦表达式和相量表达式之间是同一事物的不同表现方式。
至于为什么要转换成其他形式来表示，当然是因为正弦表达式的四则运算非常麻烦，而为了能够简便地求解正弦表达式的四则运算，我们通常将正弦表达式转换成复数来间接进行其加减运算，或者将正弦表达式转换成相量表达式来间接进行乘除运算。由于打符号很不方便，我也没法给你讲他们为什么这么转换，你只要记着怎么进行操作就行了，图片我看不太清，但可以确定的是第一道题如果是加减运算的话是要转换成正弦表达式后再转换成复数运算，而不是转换成相量。
哎，第一次给别人解释，累死我了。
3.计算：两个求和符号∑∑怎么办
先将其中一个未知数当常量，另一个未知数从1至n依次递加后各项式子相加。然后再将另一个未知数从1至n依次递加后各项式子相加便是结果。
∑ 是一个求和符号，汉语名称为西格玛（大写Σ，小写σ）。第十八个希腊字母。在希腊语中，如果一个单字的最末一个字母是小写sigma，要把该字母写成 ς ，在现代的希腊数字代表6。
大写Σ用于数学上的总和符号，比如：∑Pi，其中i=1,2,。,T，即为求P1 + P2 + 。 + PT的和。小写σ用于统计学上的标准差。西里尔字母的С及拉丁字母的S都是由Sigma演变而成。也指求和，这种写法表示的就是∑j=1+2+3+…+n。
扩展资料
求和中常见的方法有公式法、错位相减法、倒序相加法、分组法、裂项法、数学归纳法、通项化归、并项求和。在高考和各种数学竞赛中都占有重要的地位。数列求和是数列的重要内容之一，除了等差数列和等比数列有求和公式外，大部分数列的求和都需要有一定的技巧。
这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个（a1+an）、Sn =a1+ a2+ a3+。。 +an、Sn =an+ an-1+an-2。。 +a1、上下相加得Sn=(a1+an)n/2。
参考资料来源：百度百科-∑
4.求和三角函数有关的所有公式
同角三角函数的基本关系式 倒数关系： 商的关系： 平方关系： tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα sin2α+cos2α=1 1+tan2α=sec2α 1+cot2α=csc2α 诱导公式 sin（-α）=-sinα cos（-α）=cosα tan（-α）=-tanα cot（-α）=-cotα sin（π/2-α）=cosα cos（π/2-α）=sinα tan（π/2-α）=cotα cot（π/2-α）=tanα sin（π/2+α）=cosα cos（π/2+α）=-sinα tan（π/2+α）=-cotα cot（π/2+α）=-tanα sin（π-α）=sinα cos（π-α）=-cosα tan（π-α）=-tanα cot（π-α）=-cotα sin（π+α）=-sinα cos（π+α）=-cosα tan（π+α）=tanα cot（π+α）=cotα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα （其中k∈Z） 两角和与差的三角函数公式 万能公式 sin（α+β）=sinαcosβ+cosαsinβ sin（α-β）=sinαcosβ-cosαsinβ cos（α+β）=cosαcosβ-sinαsinβ cos（α-β）=cosαcosβ+sinαsinβ tanα+tanβ tan（α+β）=—————— 1-tanα ·tanβ tanα-tanβ tan（α-β）=—————— 1+tanα ·tanβ 2tan（α/2） sinα=—————— 1+tan2（α/2） 1-tan2（α/2） cosα=—————— 1+tan2（α/2） 2tan（α/2） tanα=—————— 1-tan2（α/2） 半角的正弦、余弦和正切公式 三角函数的降幂公式 二倍角的正弦、余弦和正切公式 三倍角的正弦、余弦和正切公式 sin2α=2sinαcosα cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α 2tanα tan2α=————— 1-tan2α sin3α=3sinα-4sin3α cos3α=4cos3α-3cosα 3tanα-tan3α tan3α=—————— 1-3tan2α 三角函数的和差化积公式 三角函数的积化和差公式 α+β α-β sinα+sinβ=2sin—--·cos—-— 2 2 α+β α-β sinα-sinβ=2cos—--·sin—-— 2 2 α+β α-β cosα+cosβ=2cos—--·cos—-— 2 2 α+β α-β cosα-cosβ=-2sin—--·sin—-— 2 2 1 sinα ·cosβ=-[sin（α+β）+sin（α-β）] 2 1 cosα ·sinβ=-[sin（α+β）-sin（α-β）] 2 1 cosα ·cosβ=-[cos（α+β）+cos（α-β）] 2 1 sinα ·sinβ=- -[cos（α+β）-cos（α-β）] 2。
