反比例函数的应用(反比例函数的应用知识)
1.反比例函数的应用知识
一、反比例函数的基础知识
1.一般地，形如y=(k为常数，k≠0)的函数称为反比例函数，其中x是自变量，y是函数，k是比例系数.
2.函数的解析式的特征：①等号左边是函数y，等号右边是一个分式，分子是常数k，分母中含有自变量x，且x的指数是1.②自变量x的取值范围是x≠0的一切实数.③比例系数“k≠0”是反比例函数定义的一个重要组成部分.④函数y的取值范围也是一切非0的实数.
3.反比例函数的几种等价形式：y=;y=kx-1;xy=k.(k≠0)
4.用待定系数法，求反比例函数的解析式：反比例函数 （且k为常数）中，只有一个待定系数，因此只需一对对应值就可求出k的值，从而确定其解析式.
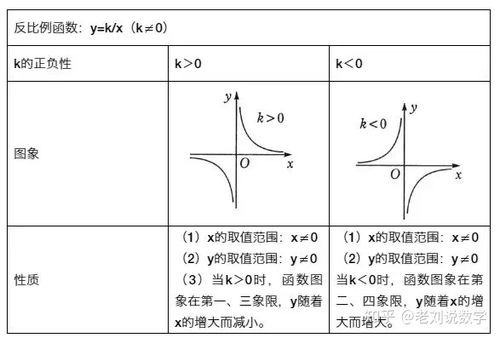
5.反比例函数y=( k为常数，k≠0)图象是双曲线.（既是轴对称图形，又是中心对称图形）
6.反比例函数图象的性质：当k>0时，双曲线位于第一，三象限，在每个象限内，曲线从左向右下降，因而y随x的增大而减小；当k<0时，双曲线位于第二，四象限，在每个象限内，曲线从左向右上升，因而y随x的增大而增大.双曲线与x轴，y轴都没有交点，而是越来越接近x轴，y轴.
7.比例系数k的几何意义：反比例函数中比例系数k的几何意义，如果过双曲线上任意一点引x轴，y轴垂线，与两坐标轴围成的矩形面积为|k|.
二、反比例函数基础知识的应用
例1. 已知 是反比例函数
(1) 求它的解析式.
(2) 求自变量 的取值范围，在每个象限内， 随 的增大而怎样变化？
(3) 它的图象位于哪个象限？
分析： （k≠0）叫反比例函数，也可以写成 ，因此，它的特点是（1）k≠0,(2)x的指数为-1.
解：（1）由题意得 ， ，解析式为
(2)自变量 的取值范围是 .
(3)由于 ，它的图象位于二、四象限；在每个象限内， 随 的增大而增大.
2.初二数学反比例函数的应用
(1)由s=vt变形得v=1500/t(2)由v=s/t=1500/15=100m/min(3)由s=vt变形得t=s/v=1500/90=1.67min
2.(1)由题中所给的数据可得到该题中x,y满足反比例函数，任找一组数据代入得y=18/x(2)由（1）y=18/x，将x=5代入，得y=3.6万元，所以2007年比2006年的每件产品少用4-3.6=0.4（万元）（3）如果用3.2万元的成本，则需要18/3.2约=5.6（万元）则需要增加投资金5.6-5=0.6（万元）
3.反比例函数关系及其应用
1.解 由题可知反比例函数解析式为
y= k/ x-0.4
且当x=0时 ，y =0.8 代入该反比例函数中得
0.8= k/ 0-0.4
∴ k= -0.32
∴y与x之间的函数关系式为 y= -0.32/ x- 0.4
2.解：当电价调至每度x元时， 本年度电力公司的收益比上年度增长20%
上年度的收益为： 1*10^8*(0.8-0.3)= 5*10^7
本年度的收益为：[-0.32/(x-0.4)]*(x-0.3)
由题得： [-0.32/(x-0.4)]*(x-0.3) = 5*10^7 *(1+20%)
解得 x= -0.39999999946667 ≈ -0.4
这题 是不是有问题
抄错了？ 第一小题就有问题啊
条件有点奇怪
4.反比例函数应用
已知点P(3,5)与点P1关于x轴对称，反比例函数的图像过点P1与P2(2,n)，求n的值
点p(3,5)与点p1关于x轴对称，
则p1((3,-5).
设反比例函数y=k/x(k≠0)
反比例函数的图像经过点p1与p2(2,n),
得方程组
-5=k/3,
且n=k/2.
解得n=-15/2.
若点A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数y=负的x分之1图像上的点，并且x1<0<x2<x3请讨论y1,y2,y3的大小关系
因为都是反比例函数y=-1/x图像的点
x1<0<x2<x3
那么y1为正，y2,y3为负
因为0<x2<x3
所以1/x2>1/x3>0
那么-1/x2<-1/x3
所以y1>y3>y2
5.反比例函数的性质与实际应用
反比例函数的最主要性质是横纵坐标之积为常数。
双曲线的性质：
⑴关于原点对称，关于第一、三象限角平分线对称，关于二、四象限角平分线对称。
⑵过双曲线上任意一点分别作X轴、Y轴的垂线段，与坐标轴构成的矩形面积等于|K|。
⑶看图象发展趋势，Y随X的增大而增大或减小。
应用：生活中反比例性质的例子非常之多：
①路程一定，时间与速度的关系，
②面积一定，长与宽的关系，
③用50元去买苹果，单价与数量的关系，
……
实际问题应当注意：自变量取值为正数，双曲线也只有一个分支。
6.初三数学 反比例函数应用
1.设A(x0,y0)
S矩形OCAD=x0*y0=2
A(x0,y0)在反比例函数y=k/x上 代入得
y0=k/x0 所以 x0*y0=k=2
所以 反比例函数是y=2/x 一次函数是y=x+2
2.联立y=2/x y=x+2 解得交点坐标为
A(-1+根号3,1+根号3) B(-1-根号3,1-根号3)
3.E(-2,0)
S△AOB=S△EOB+S△AOE
=1/2*2*（根号3-1）+1/2*2*（根号3+1）
=2根号3
